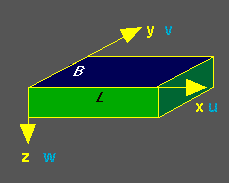
 We consider a rectangular basin of uniform depth with width B and length L filled with water. The water moves in a counter-clockwise steady motion, which means that it does not accelerate or slow down.
We consider a rectangular basin of uniform depth with width B and length L filled with water. The water moves in a counter-clockwise steady motion, which means that it does not accelerate or slow down.
 We consider a rectangular basin of uniform depth with width B and length L filled with water. The water moves in a counter-clockwise steady motion, which means that it does not accelerate or slow down.
We consider a rectangular basin of uniform depth with width B and length L filled with water. The water moves in a counter-clockwise steady motion, which means that it does not accelerate or slow down.
For convenience we assume that the long axis of the basin (the length L) points towards east and the short axis (the width B) towards north.
We assume further that there is no vertical motion, which means that the water movement is fully described by only two components, the zonal component u and the meridional component v. In other words, it is two-dimensional:
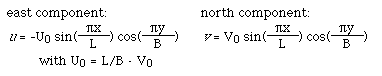
The model basin uses the values L = 40 km, B = 20 km, V0 = 0.1 m s-1 (which gives U0 = 0.2 m s-1).
The velocity thus defined is two-dimensional, which means that the vertical velocity w is identically zero. This can be verified by checking the continuity equation
The given velocity components satisfy this equation in the form
If the water movement is two-dimensional, it is possible to define a streamfunction. The streamfunction ψ is defined through the equations
With the given velocity components, ψ becomes
Streamlines are contours along which ψ is constant (the streamfunction retains the same value). For a given constant value ψ = ψ0, the co-ordinates x,y of points on the streamline are therefore given by the relationship between x and y
where the constant is given by
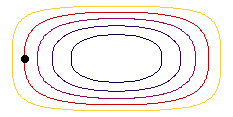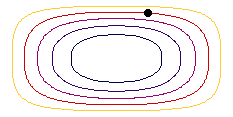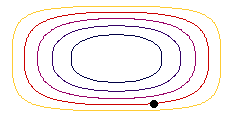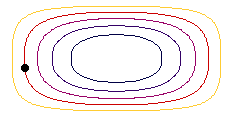 In steady movement, streamlines indicate the ways along which particles move. The animation shows the streamlines for the example of the rectangular basin in different colours and a water particle in steady state movement.
In steady movement, streamlines indicate the ways along which particles move. The animation shows the streamlines for the example of the rectangular basin in different colours and a water particle in steady state movement.
Contours which indicate the way of particles are called trajectories. Finding the trajectories for a given flow field is a Lagrangian approach to the study of currents.
We can summarize the above by saying that
Under conditions of steady flow, streamlines are trajectories. |