Exercise 1: Map projections as essential tools of physical oceanography.
Page 5
Examples of Equal Area Projections
Look at the following projections carefully and remember their properties. You will need to know them later in the exercise.
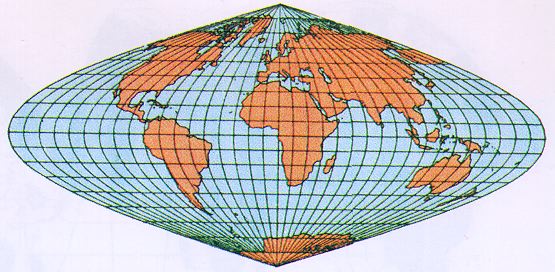
1620: The French cartographer Nicolas Sanson developed this projection, which is now named after him, from sketches left by Mercator.

1892: This projection developed by, and named after, the German cartographer Ernst Hammer has curved latitudes and longitudes.

The Mollweide projection is found in many geography texts and atlases of today; it goes back to the German mathematician Karl Brandon Mollweide (1774 - 1825).
All projections shown on this page have fidelity of area and therefore cannot have fidelity of angle. The fact that they show continents and oceans at their correct relative sizes makes them preferred map projections in geography.
A major drawback for oceanic applications are the curved meridians. They make it difficult to plot and determine positions at sea. Curved meridians also mean that it is impossible to continue maps in east-west direction. A Mollweide map of the Indian Ocean, for example, would require a redraw of the entire map.
Projections with fidelity of area are known as equal area or area conserving projections. The next page discusses equal area projections with rectangular latitude/longitude grids.
More examples of projections, both area conserving and others, can be found at the projection page of Hans Havlicek at the Technical University of Vienna (Technische Universität Wien ), from which the above example of the Hammer projection is taken by permission.
 © 2000 M. Tomczak
© 2000 M. Tomczak
contact address:
home page: http://www.es.flinders.edu.au/~mattom
web address of Exercises in Oceanography: http://www.es.flinders.edu.au/~mattom/IntExerc
This page last updated 5 December 1999


