The (Rossby) Radius of Deformation and Geostrophic flow
The radius of deformation gives us the length scale at which the geostrophic
balance (between the Coriolis and the horizontal pressure gradient forces)
will become important. You can think of it in terms of the direction of
the flow, which would in the absence of the Earth's rotation be straight
down the pressure gradient, like water gushing from a hose or flowing down
a river. Instead, in geostrophic flow, the streamlines of the flow are
deformed
by the Coriolis force, becoming parallel to the isobars (lines of constant
pressure) instead of across them. When an ocean basin is much larger than
the radius of deformation, the circulation in the interior of that ocean
will be in geostrophic balance.
Alternatively, the radius of deformation gives us the scale of features
such as fronts (distance across the front) and the width of ocean currents.
We expect these to be "close to" the radius of deformation. In oceanography,
"close to" means something like half that radius to twice that radius --
not 100 times less or 1000 times more.
Not surprisingly, the radius of deformation is heavily dependent on
the stratification (or how density changes with depth) and the Coriolis
parameter. The equation for the radius of deformation is:
R_bc = sqrt(g' * D1) / f
where D1 is the depth of the upper
layer of the ocean (above the pycnocline), and g'
is reduced gravity, which is given by:
g' = g (r_2 - r_1)/r
where r_1 and r_2
are the densities of the upper and lower layers, respectively, r
is
the mean density,g = 9.81 m/s^2, and
f
is the Coriolis parameter.
Problem 10
-
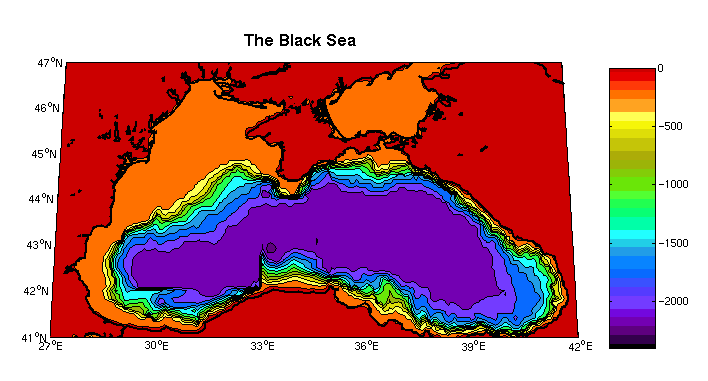
Using the following data, please calculate the Rossby radius of deformation
for the Black Sea. Show all of your work. You can use the mean latitude
of the Black Sea (about 43N). Give me your answer in kilometers. Note that
the density field (here displayed using sigma-t) is given by the solid
line in the middle panel, and the dashed line in the same paenl is your
old friend E, the stability parameter. Please justify
your choice of the depth of the upper layer. What parameter or parameters
did you use to decide?
-
Given this information, do you expect flow in the Black Sea be largely
geostrophic?
-
How wide is the Black Sea compared to the radius of deformation?
-
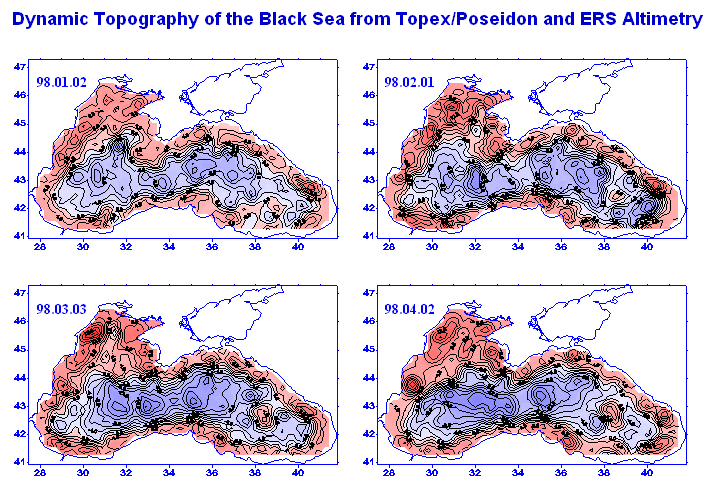
Take a look at the last image, which is sea surface height measured by
a satellite. The rim current is clearly visible, as the crowded black lines
of constant sea surface height (which can be thought of as isobars or as
contours of dynamic height) around the edge of the Black Sea. How does
the width of the rim current compare with the radius of deformation here?
-
Is it what you expected? Why or why not?