Don't forget in all of this that the Coriolis force is just an artifact of our desire to look at things in a geo-centric perspective. It's not a real force at all.

Using the transect below, you're going to calculate the geostrophic velocity based on the thermal wind equation:

Again, remember that dp/r is simply equal to the dynamic height, H, related through the hydrostatic equation (dp/dz = -rg).  You will want to calculate that first, as an interim step. d(H)/dx is then the horizontal change in H, or the difference between H at one station versus another.  Remember that to calculate the horizontal change in H correctly, you must use the same reference level for both stations and you must compare value of H at the same pressure levels at each station!  We use dH to indicate such a horizontal difference.  Note: Often oceanographers use notation like this H(0/1000), or H(50/2000) to indicate the pressure level being considered and the reference level. The first example would be for dynamic height at the surface calculated relative to 1000 dbar, and the second example, dynamic height at 50 dbar relative to a reference level of 2000 dbar.

When calculating geostrophic velocity from hydrographic stations, dx, the horizontal differential, is simply the distance between stations or L. You can try to measure L from the figure or simply use the average station spacing for this transect, which was 9 km. Rearranging our first equation using H and L, we get, simply:

Where dH  is the difference in dynamic height (at a given pressure level) between the two stations separated by distance L. But remember, this is all based on the premise that at some depth, designated as the reference level, the horizontal pressure gradient force is zero and the currents die away. Thus to get a velocity at any depth you will have to integrate (sum) all of the dynamic heights from that reference level up to the level of interest to you.

Part I

1. Examine the transect, and estimate the dynamic height at each station for 0,10,20,30 and 40 dbar relative to 55 dbar. Remember that while the surface of the ocean is shown as flat it's not! This is an effect of using pressure as the vertical coordinate.
2. From the dynamic heights, and using a mean latitude for this transect of 43 degrees 30'N, calculate the geostrophic velocity between each station pair at 0,10,20,30 and 40 dbar. Which way is the current going and how strong is it? Orient your answer in terms of the figure (i.e., to the left, to the right, up, down, into the picture, out of the picture). Why do you have to use a pair of stations? Why can't we calculate the geostrophic velocity at a given station?
3. Now for the two stations furthest to the right, calculate the surface dynamic height and surface geostrophic velocity relative to 120 dbar and also relative to 55 dbar. What is the difference in surface dynamic height between these two stations using these two levels?
4. What does that say about the strength of the currents between 55 and 120 dbar at this location? (Think relatively: if the surface velocity is 10 cm/s relative to the velocity at 55 dbar, and the water at 55 dbar turns out to be moving at 4 cm/s, how fast is the surface current actually moving?)
5. Do you think your estimate of the surface velocity would change much if you used a reference level of 160 dbar instead of 120? Why or why not?
6. BONUS QUESTION: What does your answer to the preceding questions say about the use of geostrophic calculations for in this area? Is there a motionless "reference" depth that's common to all the stations? If you think so, what depth is it? If not, what might you do to compensate? Defend your answer.

 

 
 
 
 
 

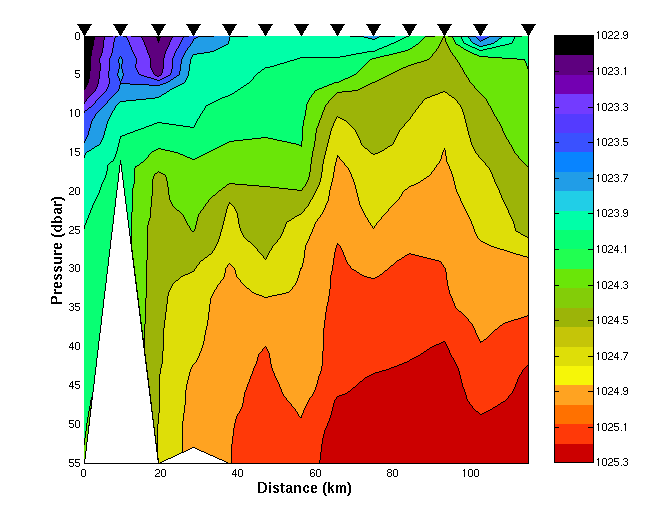
In this figure, the black triangles indicate the station locations, and the black line, the 55 dbar reference depth. Potential density (sigma_theta + 1000 ) is contoured in color. In the second figure down, the the top 55 dbar of the same transect is pictured, with the color table stretched for maximum contrast.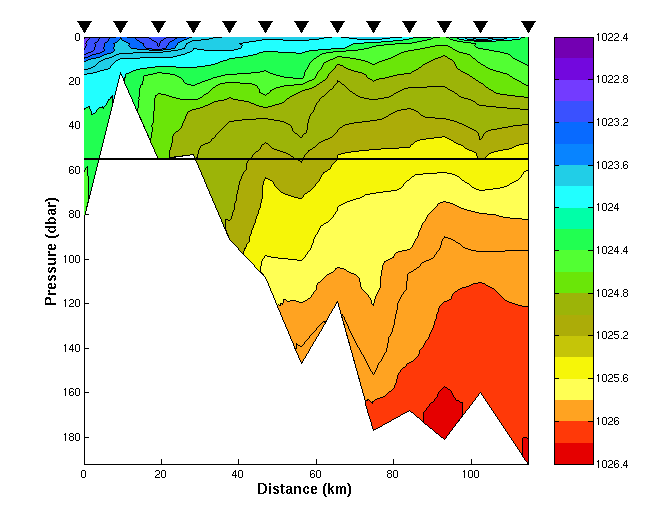

Part II