Using the hydrostatic equation: and the following two hydrographic casts, which were collected just outside of Penobscot Bay, Maine on the R/V Cape Hatteras in June, 1998 as part of the ECOHAB project. 

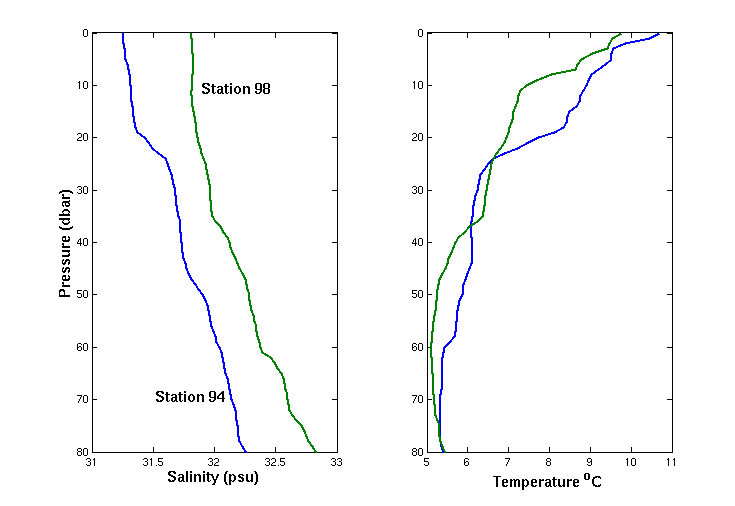
1. For each station, calculate the dynamic height at 0, 10, 20, and 50 dbar relative to 80 dbar. Click here to download a table  of the Potential Density, which you will need to make the calculation. Give your answer in dynamic meters (1 dyn. m. = 10 m^2/s^2). Remember, dynamic height, DH, is g * dz , and when given in dynamic meters will be approximately the same as the height (in meters) above the reference level . You should use a spreadsheet like Excel or a scientific programming environment such as Matlab or IDL to calculate this. I don't want to find out you did it by hand!
2. Where does difference in dynamic height from station 94 to 98 change most quickly with depth? Most slowly? How is this related to the stratification?
3. What is sigma(S,T,p) at 0,10,20,50 and 80 dbar? This will simply be the in situ density minus 1000 kg/m^3. Note: in your web browser, the Greek symbol for density looks like this: r. You might want to use this calculator to help you answer the question.
4. What is sigma_t(S,T,0)  at 0,10,20,50 and 80 dbar? Is it a higher or lower number than sigma(S,T,p) at the corresponding depth?
5. What is sigma_theta(S,theta,0) at these same pressures? How does it compare to sigma and sigma_t? Note: You can calculate sigma_theta in one of two ways. One, you have the software to do it in one step from S, T, and p. Two, you first calculate the potential temperature, theta, (perhaps using this calculator) and then you plug in S and theta into the calculation of sigma_t (perhaps using this calculator). The result will be exactly the same, in other words, sigma_t(S,theta,0) == sigma_theta(S,T,0).
6. Now assuming that the horizontal pressure gradient force goes to zero at 80 dbar (in other words, the 80 dbar pressure surface is exactly level), what is the horizontal pressure gradient force at 0,10,20 and 50 dbar from at Station 94 to station 98, given that the stations lie 37 km apart (L = 37,000 m)? Note: You already have everything you need to calculate this answer!

 
• The horizontal pressure gradient is 1/r * dp/dx, which is (dp/r)/dx which, as you can see from of the hydrostatic equation above is just the change in dynamic height from one station to the other divided by the distance between stations -- remember H == g*dz == dp/r. Thus the horizontal pressure gradient force = H / L.. Please give your answer in m/s^2, and do note that this is an acceleration.
7. At which of the selected depths (0,20,50,80) is the pressure gradient force the strongest? At which is it the weakest? At each of these depths, in which direction is it oriented, from station 94 to 98, or the other way around?